SchNet: A Continuous-filter convolutional neural network for modeling quantum interactions

Paper Summary: SchNet: A Continuous-filter convolutional neural network for modeling quantum interactions

We propose SchNet: a neural network specifically designed to respect essential quantum chemical constraints. SchNet delivers both rotationally invariant energy prediction and rotationally equivariant force predictions.

OUTLINE:

I. Background
II. Key contributions
III. Proposed architecture of SchNet
IV. Remarks from the experiments
V. Opinion

I. Background

분자의 특성을 예측하는 것은 목적에 맞는 새로운 분자를 디자인하는데 필수적이다. 가령 약물 분자를 디자인 한다면, 분자의 독성이나 용해도 등을 예측해야 할 것이다. 하지만 탐색 가능한 분자의 공간(chemical space)은 너무나 넓어, 이러한 특성을 만족하는 분자를 실험이나 ab-initio 양자 계산을 통해 찾는 것은 시간적으로나 금전적으로 큰 부담이 된다. 따라서, 최근(참고로 이 논문은 2017년도 논문이다.)에는 딥 러닝을 이용한 분자의 특성을 예측하는 방법이 떠오르고 있다. 특히, 이번 포스팅에서는 분자의 3차원 구조를 다루는 방법에 초점을 맞춰 알아볼 것이다.

주어진 3차원 분자를 나타내는 방법(representation)에는 어떤 것들이 있을까? 제일 간단한 표현법은 아마도 3차원 격자(grid)를 이용한 방법일 것이다. 각각의 격자가 일정 간격으로 떨어진 3차원 공간상의 $(x,y,z)$ 좌표를 나타내며, 원자의 정보를 그 위치에 해당하는 격자에 넣어줌으로서 분자를 표현할 수 있다. 이러한 표현법은 3차원 convolutional neural network(3D CNN)을 통해 원하는 특성을 예측하는데에 사용할 수 있다.

하지만 3D CNN을 분자에 사용하는데에는 크게 네 가지 문제가 있다. 첫 번째는, 격자 형태로 좌표를 나타내게 되면 위치의 분포가 불연속적이게 된다는 것이다. 격자의 간격을 좁히면 보다 높은 해상도로 분자를 표현할 수 있겠지만, 사용되는 표현법의 크기는 $O(n^3)$으로 해상도를 높이는 데에는 한계가 있다. 두 번째는, 모델이 input의 크기에 대해 scalable하지 않다. 이는, 학습할 때 사용한 격자의 전체 크기를 초과하는 분자는 예측의 input으로 사용할 수 없음을 의미한다. 또한, 3D CNN은 rotation에 대해 equivariant하지 않다. Equivariance에 관한 내용은 이 링크를 참고하자. 이는 주어진 분자의 좌표가 공간상에서 회전하게 되면 원자들의 상대적인 위치는 같더라도 모델이 다른 결과를 예측하게 한다. 마지막으로, 분자를 격자로 나타내면 분자내의 결합(bonding)에 관한 정보를 포함할 수 없다.

또 다른 표현법으로는 그래프(graph)를 사용할 수 있다. 그래프 $G = (V, E)$는 node $v_i\in V$와 edge $e_{ij}\in E$로 이루어져있으며, 분자에서 node는 원자, edge는 원자간 결합 또는 상호작용을 의미한다. 원자 사이의 거리 $d_{ij}=\Vert\mathbf{r}_i-\mathbf{r}_j\Vert_2$를 edge 정보로 활용(거리를 일정 간격으로 나누어 one-hot vector로 만들 수 있다)하면 분자의 3차원 정보를 담을 수 있다. 이렇게 표현된 분자 그래프는 graph neural network(GNN)을 통해 물성을 예측할 수 있다. 그래프 표현법의 장점은 roto-translation에 대해 equivariant하며, 원자들 사이의 pairwise feature(거리, 결합 정보 등)를 모델 학습에 제공해 줄 수 있다는 것이다. 다만, 앞서 3D CNN의 문제점으로 이야기한, 거리의 불연속적인 표현은 여전히 해결되어야 할 문제이다.

II. Key contributions

1. 본 논문에서, 거리를 one-hot vector로 표현했을 때 불연속적으로 표현되는 것을 해결하기 위해 radial basis function을 이용해 거리를 연속적으로 표현하였다. 아래 식에서 $\mu_k$는 중앙값으로 $0Å\leq\mu_k\leq30Å$ 을 $0.1Å$ 간격으로 사용하였다. $\gamma$의 값으로 $10Å$을 사용하였다. 이러한 continuous-filter를 통해 아래 그림과 같이 분자 구조의 연속적인 표현을 가능하게 해준다.

   $$e_ k(\mathbf{r}_ i-\mathbf{r}_ j)=exp(-\gamma\Vert d_ {ij}-\mu_ k\Vert^2)$$

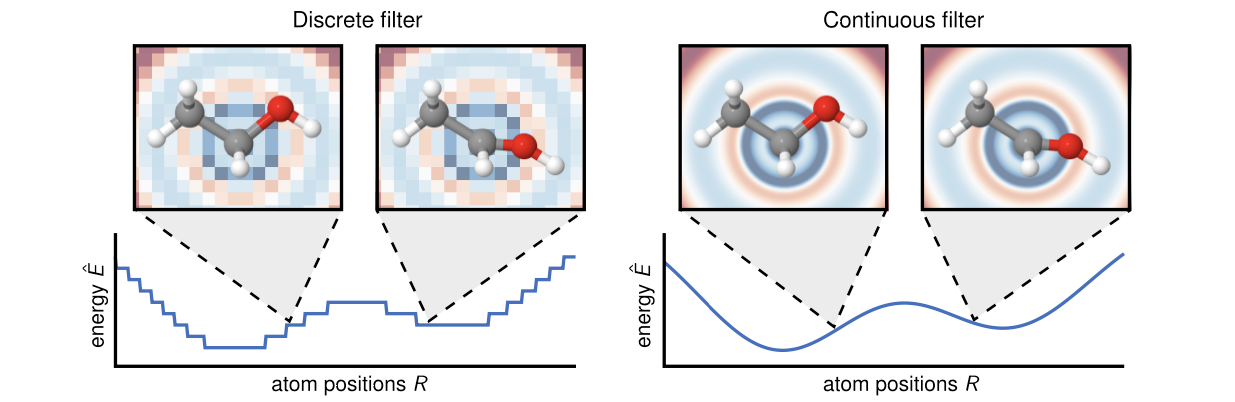
2. 본 논문에서는 SchNet을 소개하며, input으로 원자의 3차원 좌표인 $\mathbf{r}_i \in \mathbb{R}^3$를 사용한다. 에너지의 위치에 대한 gradient는 힘이라는 사실을 loss로 사용하여 energy-conserving force model을 설계하였다.

$$\mathbf{F}_i(\mathbf{r}_1,…,\mathbf{r}_n)=-\frac{\partial E}{\partial {\mathbf{r}_i}}(\mathbf{r}_1,…,\mathbf{r}_i)$$

3. ISO17이라는 새로운 벤치마크 데이터셋을 제공한다. $C_7O_2H_{10}$의 분자식을 갖는 129개의 isomer들의 MD trajectory 각 5,000개를 담은 이 데이터셋은, PES 상의 local minima에 있는 분자들로 모델을 학습했을 때 *non-equilibrium conformer*에 대해 얼마나 에너지를 정확하게 예측하는지 모델의 generalization을 평가할 수 있게 해준다.

III. Proposed architecture of SchNet

SchNet의 구조는 아래 그림과 같다. $n$개의 원자로 이루어진 분자에서, 각 원자의 전하량 $Z=(Z_1,…,Z_n)$과 각 원자의 위치 $R=(\mathbf{r}_1,…,\mathbf{r}_n)$를 모델의 input으로 사용한다. $Z$는 embedding layer를 통해 feature vector $\mathbf{x}^l_i\in \mathbb{R}^F$의 집합 $X^l=(\mathbf{x}^l_1,…,\mathbf{x}^l_n)$로 embedding 된다.

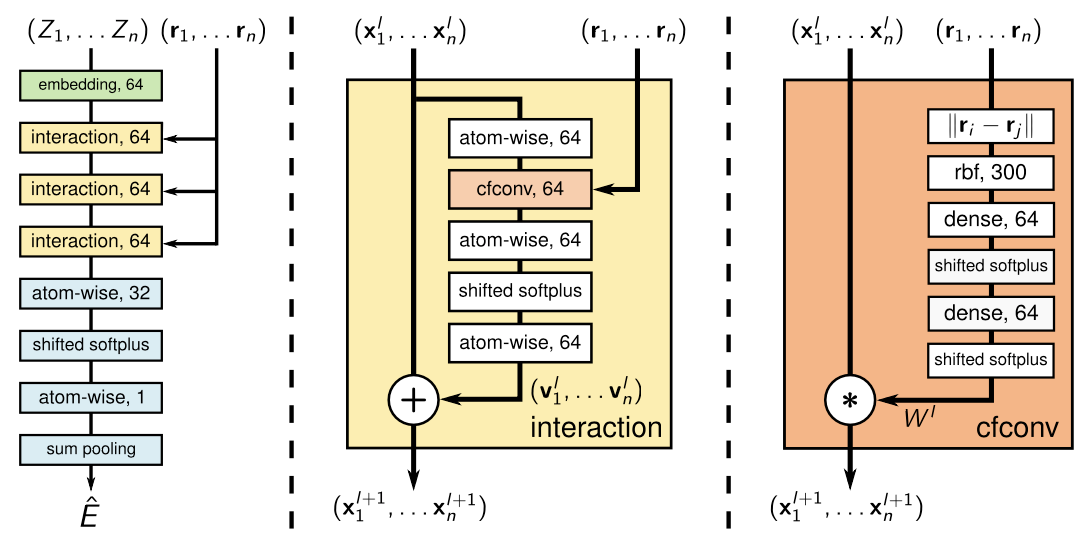
1. Continuous-filter Convolutional (cfconv) layer

   $R$로부터 계산한 $d_{ij}=\Vert\mathbf{r}_i-\mathbf{r}_j\Vert$를 위에서 소개한 식과 같이 RBF로 expand 한다. 아래 식에서의 $W^l$이 filter-generating 함수이다. 이를 $X^l$와 element-wise product하여 다음 layer의 feature vector를 얻는다.

   $$\mathbf{x}_i^{l+1}=(X^l*W^l)_i=\sum_j\mathbf{x}^l_j\circ W^l(\mathbf{r}_i-\mathbf{r}_j),W^l:\mathbb{R}^3\to\mathbb{R}^F$$

   여기서 activation function으로 shifted softplus 함수를 사용하였는데, 이때 $ssp(0)=0$이며 무한 번 미분 가능하다는 성질을 가지고 있다.

   $$ssp(x)=ln(e^x+1)-ln(2)$$

2. Interaction Blocks

   SchNet은 총 3개의 interaction block을 사용하였다. 기본적으로 residual connection 구조로 되어있는 interaction block은 cfconv layer를 통해 얻은 $V^l=(\mathbf{v}_1^l,…,\mathbf{v}_n^l)$을 $X^l$와 합하여 다음 layer의 feature vector를 얻는다. 여기서 atom-wise layer는 feature dimension에서의 linear layer이다.

3. Loss Function

   모델이 예측한 에너지 $\hat{E}$를 각 원자의 위치 $\mathbf{r}_i$에 대해 미분하면 각 원자에 작용하는 힘 $\hat{\mathbf{F}}_i$을 구할 수 있다.

   $$\hat{\mathbf{F}}_i(Z_1,…,Z_n,\mathbf{r}_1,…,\mathbf{r}_n)=-\frac{\partial\hat{E}}{\partial {\mathbf{r}_i}}(Z_1,…,Z_n,\mathbf{r}_1,…,\mathbf{r}_i)$$

   이를 loss function에 추가하여 실제 힘이 label로 주어졌을 때 보다 정확한 PES $\hat{E}(\mathbf{r}_1,…,\mathbf{r}_n)$를 예측할 수 있도록 해주었다. 여기서 $\rho=0.01$을 사용하였다.

   $$l(\hat{E},(E,\mathbf{F}_ 1,…,\mathbf{F}_ n))=\rho\Vert E-\hat{E}\Vert^2+\frac{1}{n}\sum_ {i=0}^{n}\left\Vert\mathbf{F}_ i-\left(-\frac{\partial\hat{E}}{\partial{\mathbf{r}_ i}}\right)\right\Vert^2$$

IV. Remarks from the experiments

본 논문에서는 세 가지 데이터셋으로 모델을 평가하였다.

1. QM9

   QM9은 C, N, O, F로 이루어진 약 13만개의 분자들의 equilibrium 구조를 가지고 있다. 정의에 의해 $\mathbf{F}=0$으로 놓고 학습하였다. 에너지 예측에서 SchNet이 다른 모델에 비해 더 낮은 MAE를 보여주며 state-of-the-art performance를 기록하였다.

2. MD17

   MD17은 8개의 유기 분자들의 MD trajectories를 포함하고 있다. 아래의 결과로부터 두 가지 결론을 얻을 수 있다. 먼저, energy만 가지고 학습한 SchNet보다 force를 함께 사용하였을 때의 성능이 월등히 좋아지는 것을 확인 할 수 있었다. 또한, 샘플의 수가 적을 때($N=1,000$)는 SchNet보다 gradient-domain machine learning(GDML)이 더 나은 성능을 보여주지만 GDML은 scalable하지 않아 원자의 수가 많거나 데이터 샘플의 수가 많은 경우에는 사용하기 힘들다. 반면, SchNet은 샘플이 많은 경우($N=50,000$)에서 더 좋아진 성능을 보여주었다.

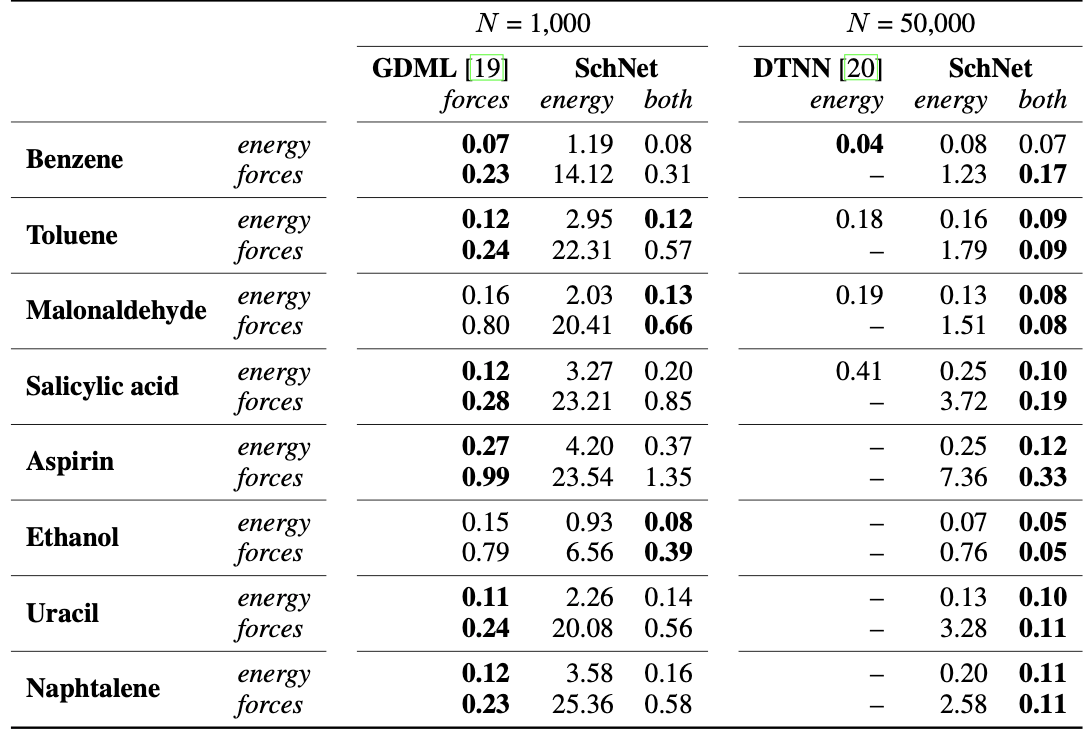
3. ISO17

   ISO17에 대해서는 두 가지 실험을 진행하였다. 첫 번째는, train에서 사용한 분자가 test set에 있지만 구조가 다른 경우, 두 번째는 train에서 사용한 분자가 test set에 포함되어 있지 않은 경우이다. 전자는 얼마나 모델이 conformation 변화에 따른 PES를 잘 예측하는지, 후자는 얼마나 모델이 보지 못한 분자에 대해 generalize를 잘하는지 평가한다. 아래 표의 결과와 같이, energy와 force를 함께 사용하여 학습한 경우가 두 실험 모두에서 좋은 결과를 보여주었다.

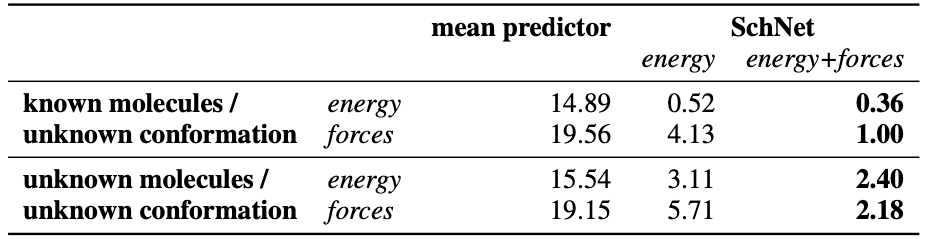
5. Opinion

본 논문에서는 continuous-filter generating function을 통해 거리 정보를 연속적인 벡터로 embedding하면서 3차원 분자 구조에 대한 정보를 효과적으로 분자 물성 예측에 활용하였다. 또한, 힘-에너지 관계식을 통해 모델이 에너지를 예측하는 동시에 주어진 구조의 각 원자에 미치는 힘을 맞추게 하여 분자의 conformation에 따른 PES를 학습하도록 한 점이 인상적이었다. 또한, convolution하는 과정에서 모든 원자에 대해 동등한 비율로 summation을 하는데, 중요도를 함께 학습하여 weighted-sum을 하면 효과적일 것으로 생각된다. 다만, loss를 구하는 과정에서 derivative를 구하는 과정이 많은 계산량을 요하며, 모델이 roto-translation에 invariant하여 equivariant한 벡터 예측에는 적용하기 어렵다는 단점이 있을 것으로 생각된다.

$$***$$