Concrete Dropout

Paper Summary: Concrete Dropout

1. Intro

모델의 예측 불확실성(uncertainty)를 잘 calibrate 하는 것은 자율 주행과 같은 심층 학습 문제에서 굉장히 중요하다. 이를 위한 한 가지 방법이 dropout을 이용한 Bayesian inferencing이다. 이는 학습 과정 뿐 아니라 test time에서도 dropout을 하여 모델의 predictive distribution을 만드는 방법이다. 하지만 이를 잘 수행하기 위해서는 dropout의 확률을 잘 calibrate하여야 하는데, 보통 이는 grid-search 방법을 통해 수행되었다. 하지만 이방법에는 한계점이 있는데, 일단 많은 시간과 계산 자원이 필요하며, dynamic하게 dropout 확률이 변해야하는 상황(e.g. RL)에는 적용이 불가능하다는 것이다. 따라서, 좋은 모델 성능과 uncertainty 예측을 위해 dropout 확률을 모델 학습 과정에서 최적화하는 방법이 필요하다.

본격적인 내용에 들어가기에 앞서, 사전 지식으로 model uncertainty에 대해 짚고 넘어가자. Model uncertainty는 크게 epistemic uncertainty와 aleatoric uncertainty로 나뉠 수 있다. 간단하게 이야기하면, 전자는 모델에서 발생하는 uncertainty이며 후자는 데이터에서 발생하는 uncertainty이다. Epistemic uncertainty는 모델을 앙상블하여 그 variance를 통해 estimate 할 수 있으며 aleatoric uncertainty는 학습 과정에서 data variance를 함께 학습하여 estimate 할 수 있다. 이 두 uncertainty를 합한 것이 predictive uncertainty이다.

2. Main Contributions

본 논문에서는 concrete dropout이라는 새로운 Bayesian inferencing method를 소개한다. Dropout 확률이 gradient method로 학습되는 방법이며, 이를 통해 더 나은 uncertainty calibration을 할 수 있다고 주장한다. 먼저 방법론과 관련 이론들을 살펴보자.

Dropout 확률을 학습시키기 위해서는 dropout의 variational interpretation으로부터 출발해야한다. Dropout을 사용하면 $L$개의 layer를 가진 random weight matrices의 set $w=\{W_l\}^L_{l=1}$와 variational parameters의 set $\theta$에 대해서, 분포 $q_\theta (\omega)$를 Bayesian NN의 posterior로 approximate 할 수 있다. 이때 최소화해야하는 objective function은 아래와 같다.

$$\hat{L}_ {MC}(\theta) = -\frac{1}{M}\sum_{i\in{S}}logp(y_{i}|f^\omega(x_i))+\frac{1}{N}KL(q_\theta(\omega)||p(\omega))$$

여기서 $N$은 데이터의 개수, $S$는 $M$개의 데이터를 갖는 random set, $f^\omega (x_i)$는 model output이다. KL divergence term은 regularisation을 위한 term으로, posterior가 prior distribution $p(\omega)$으로부터 너무 벗어나지 않도록 해준다. 이때 variational parameters의 set $\theta$이 dropout 분포에 대해 $\theta=\{M_l,p_l\}^L_{l=1}$을 만족한다고 가정하다. 이때 $M_l$은 mean weight matrix, $p_l$은 dropout 확률이며 아래와 같은 식을 만족한다. 여기서 $W_l$의 dimension은 $K_{l+1}\times K_l$이다.

$$q_\theta(\omega)=\prod_{l}q_{M_l}(W_l), q_{M_l}(W_l)=M_l\cdot diag[Bernoulli(1-p_l)^{K_l}]$$

위 식을 조금만 깊이 살펴보자. $w={{W_l}}^L_{l=1}$으로부터 $q_\theta (\omega)$가 분해될 수 있으며, 이때 $q_{M_l}(W_l)$은 matrix $M_l$에서 0 또는 1을 주어진 확률로 뱉어주는 Bernoulli distribution을 통과시켜줌으로서 얻는 $l$번째 layer의 distribution이다. 이를 이용하여 위의 KL term을 다시 적어보면,

$$KL(q_\theta(\omega)||p(\omega))=\sum^{L}_{l=1}{KL(q_{M_l}(W_l)||p(W_l))}$$

$$KL(q_{M}(W)||p(W))\propto\frac{l^2(1-p)}{2}||M||^2-K\cdot BCE(p)$$

$$BCE(p):=-plogp-(1-p)log(1-p)$$

이와 같이 정리할 수 있다. (https://mlg.eng.cam.ac.uk/yarin/thesis/thesis.pdf 참조) 자세한 유도 과정까지는 이해하지 못했지만, 결국 골자는 이렇게 식을 정리하면 objective function에 dropout probability인 $p$가 들어가게 되며, gradient method를 이용하여 $p$를 optimization 시킬 수 있다는 것이다. Binary cross entropy term은 dropout regularisation term이며, dropout probability를 최대값인 0.5로 가게끔 해준다. 큰 모델 (large $K$) 일수록 그 효과는 커지며, 데이터의 개수가 많을수록 (large $N$) $p$는 0에 가까워질 것이다.

하지만 여기서 Bernoulli distribution을 사용하는데에 문제가 있다. Bernoulli distribution은 discrete하여, 이를 back-propagation을 위한 $g(\theta,\epsilon)$의 형태로 re-parameterize 하는 것이 불가능하다($\theta$는 distribution의 parameter, $\epsilon$은 $\theta$에 의존하지 않는 random variable). 따라서, 이 논문에서는 Concrete distribution relaxation을 사용하였다.

Discrete한 random variable을 근사하기 위한 한 가지 방법인 Gumbel-softmax trick에 대해 알아보자. Gumbel distribution은 $F(x;\mu,\beta)=e^{-e^{-(x-\mu)/\beta}}$으로 $\mu$와 $\beta$를 파라미터로 갖는다. Standard Gumbel distribution $F(x;0,1)$에서 ${{\epsilon_i}}^k_{i=1}$을 sampling하고, categorical 분포의 확률 변수를 ${{\pi_i}}^k_{i=1}$라고 했을 때, $z=argmax_i[log(\pi_i)+\epsilon_i]$로 정의하자. 이때, $p(z=k)=\pi_k$가 되는 것이 Gumbel distribution의 성질이다. 하지만, argmax 또한 differentiable하지 않으므로, softmax로 이를 바꿔준다. 즉, $z=softmax_i[log(\pi_i)+\epsilon_i]$로 나타내며 아래 식과 같이 표현될 수 있다. 여기서 $\tau$는 uniformity를 결정해주는 temperature parameter이다.

$$y_i=\frac{exp((log\pi_i+\epsilon_i)/\tau)}{\sum^k_{i=1} exp((log\pi_i+\epsilon_i)/\tau)}$$

이 논문에서 사용된 Concrete distribution은 uniform distribution에서 sampling한 $u\sim Unif(0,1)$에 대해 아래 식과 같이 $z$를 정의한다. 마찬가지로 $\tau$는 temperature parameter이다.

$$z=\sigma\left(\frac{1}{\tau}\cdot(logp-log(1-p)+logu-log(1-u))\right)$$

이러한 discrete random variable에 대한 re-parameterization trick을 통해 $p$를 학습시킬 수 있다.

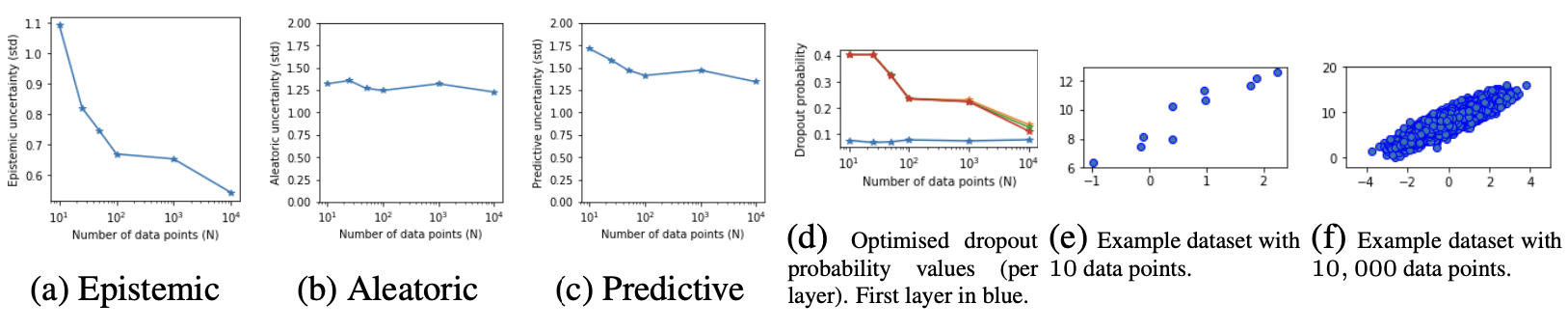
이제 결과를 살펴보자. 먼저, synthetic data에 대한 분석이다. 데이터의 개수가 늘어남에 따라 epistemic uncertainty는 감소하며, aleatoric uncertainty는 이에 영향받지 않음을 확인할 수 있다. 또한, (d)에서 dropout probability가 데이터 개수가 증가함에 따라 hand-tune 했을 때와 같은 경향으로, 점차 0에 가까워지는 것을 확인할 수 있다.

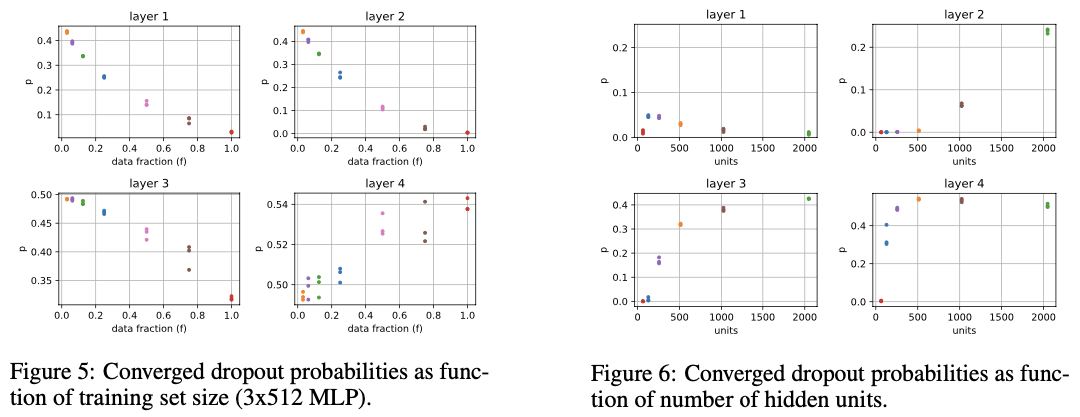
MNIST benchmark에 대해서도 test를 하였는데, model size와 dataset size를 바꿔가며 각 layer 별 dropout parameter를 plot하였다. 데이터셋 크기가 커질수록 첫 두 layer의 $p$가 0으로 수렴하였으며, 이는 위 실험의 결과와 일치한다. 또한, 모델의 크기가 커질수록 epistemic uncertainty가 증가하며, 이에 따라 $p$ 또한 커지는 것을 확인할 수 있었다.

다음은 sementic segmentation task에서의 방법에 따른 모델 성능(Intersection over Union; IoU)을 비교하였다. MC sampling을 하지 않은 경우보다 한 경우 IoU가 더 높았으며, Concrete dropout을 사용한 모델이 $p$를 고정하였을 때 보다 조금 더 좋은 결과를 보여주었다. 또한, uncertainty calibration 면에서도 Concrete dropout 모델의 RMSE 값이 가장 낮았다.

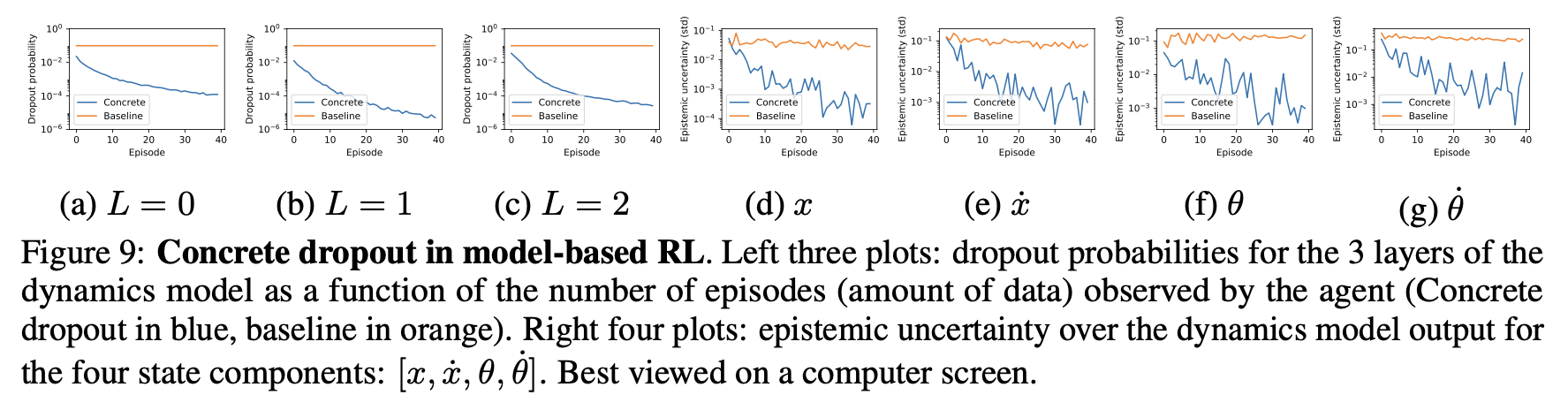
마지막으로 multi-episode RL에서 Concrete dropout을 적용하여 episode가 진행됨에 따른 $p$와 epistemic uncertainty를 분석하였다. 점점 더 많은 데이터가 수집되면서, $p$가 점점 감소하는 것을 확인할 수 있었다. 또한, Cartpole example에서의 $x,\dot{x},\theta,\dot{\theta}$에 대한 epistemic uncertainty가 episode가 진행되면서 점차 감소하는 것을 확인할 수 있었다.

3. Opinion

Bayesian inferencing에 관련된 논문들 중에서 가장 궁금했던 논문이었다. 항상 hyper-parameter로만 생각해왔던 dropout ratio를 gradient method로 optimize 한다는 아이디어가 정말 독창적이라고 생각했다. Calibrate 된 $p$를 통해 기존의 uncertainty와 dataset size, model size간의 관련성을 설명할 수 있었으며, hand-tune 하는 것보다 나은 model 성능을 얻을 수 있었던 것에서 이 방법론의 활용 가치가 충분하다고 생각한다. Concrete distribution 대신 Gumbel distribution으로 $p$를 re-parameterize하면 성능에 어떻게 영향을 미칠지 궁금하다.

$$***$$