Bayesian Deep Learning and a Probabilistic Perspective of Generalization

Paper Summary: Bayesian Deep Learning and a Probabilistic Perspective of Generalization

1. Intro

“From this probabilistic perspective, it is crucial not to conflate the flexibility of a model with the complexity of a model class.”

고전적으로 파라미터의 수가 많으면 모델이 데이터셋에 overfit 될 수 있으며 이는 generalization의 감소로 이어질 수 있다고 생각되어왔다. 하지만 Gaussian process와 같이 non-parametric한 방법은 무한히 많은 파라미터를 사용하는 것과 같지만 여전히 넓은 범위의 데이터에 대하여 좋은 모델 유연성(flexibility)을 보여준다.

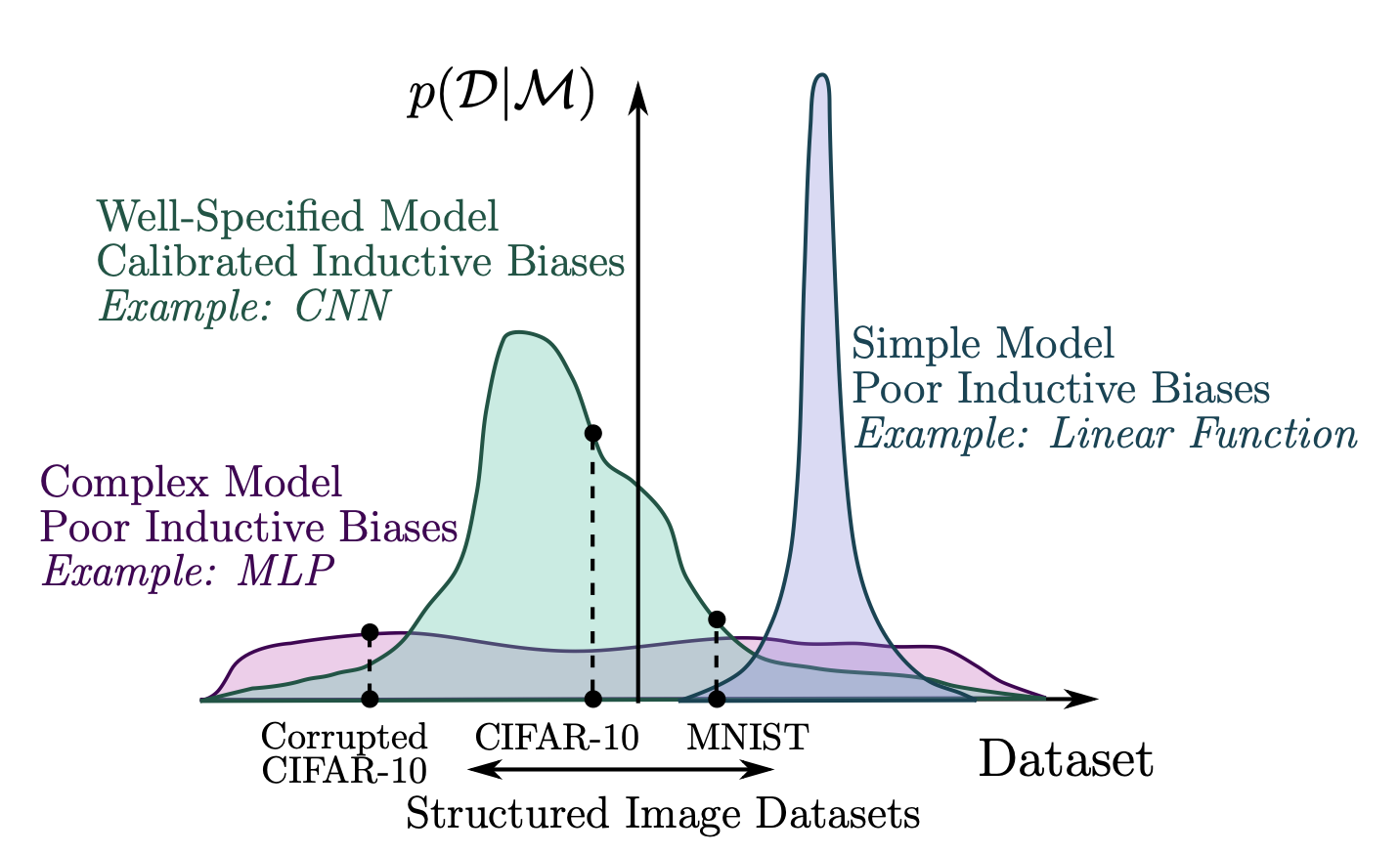
이 논문에서는 모델의 generalization을 probabilistic 관점에서 크게 두 가지에 의존한다고 이야기한다. 첫 번째는 support로, evidence > 0인 데이터셋의 범위, 즉 모델의 expressive power를 이야기한다. 선형 모델의 경우 support는 매우 한정적이지만, NN과 같이 아주 많은 파라미터를 사용할 경우 support는 넓어지게 된다.

두 번째는 inductive bias로, support의 분포, 즉 다른 데이터셋에 대해 모델이 얼마나 다른 prior probability를 갖는지를 이야기한다. 예를 들어, CIFAR-10과 corrupted CIFAR-10 데이터셋이 있을 때, MLP 모델과 CNN 모델을 비교해보자. 두 모델 모두 넓은 support를 가지고 있지만, MLP 모델에 비해 CNN 모델이 주어진 데이터에 대한 합당한 inductive bias를 가지고 있어서 두 데이터셋을 구분해낼 수 있다. 이러한 관점에서, 모델의 generalization이라는 것은 단순한 모델 complexity 만의 문제가 아닌, support와 inductive bias를 모두 고려해야 한다.

Bayesian 모델의 가장 큰 특징은 optimization이 아니라 marginalization이라는 것이다. 이 말이 무슨 뜻이냐하면, 한 가지 파라미터들로 주어진 input에 대한 output을 결정하는 것이 아니라 각각 분포를 갖는 파라미터에 의해 결정되는 posterior probability로 weighted 되는 output의 marginal이라는 것이다.

$$p(y|x,D)=\int{p(y|x,w)p(w|D)dw}$$

위 식이 이 의미를 잘 내포하고 있는데, $p(y|x,D)$는 주어진 input $x$와 data $D$에 대해 output $y$가 나올 조건부 확률이며 이는 주어진 $x$와 parameter $w$에 대해 $y$가 나올 확률을 posterior $p(w|D)$로 weighted sum한 것임을 보여주고 있다. 여기서 $p(y|x,D)$를 Bayesian model average (BMA)라고 한다.

최근에 uncertainty representation에서 gold standard로 주목받고 있는 deep ensemble은 dataset으로부터 sampling한 sub-dataset들로 학습한 여러 모델들의 평균값을 내준다. 이 방법은 아래의 Monte Carlo approximation과 비슷하게 marginalization을 통해 위 식의 적분식을 계산 가능하게 해준다. 또한, 기존 Bayesian NN들에 비해 추가적인 파라미터나 긴 학습 시간을 필요로 하지 않는다는 장점이 있다.

$$p(y|x,D)\approx \frac{1}{J}\sum^{J}_{j=1}{p(y|x,w_j)},w_j\sim p(w|D) $$

2. Main Contributions

이 논문에서는 deep ensemble을 이용한 MultiSWAG를 제안하였다. Deep ensemble이 Bayesian marginalization으로 근사될 수 있음을 보였으며, 이를 통하여 기존의 Bayesian 모델들보다 Bayesian predictive distribution을 더 잘 예측할 수 있다는 것을 실험적으로 보여주었다.

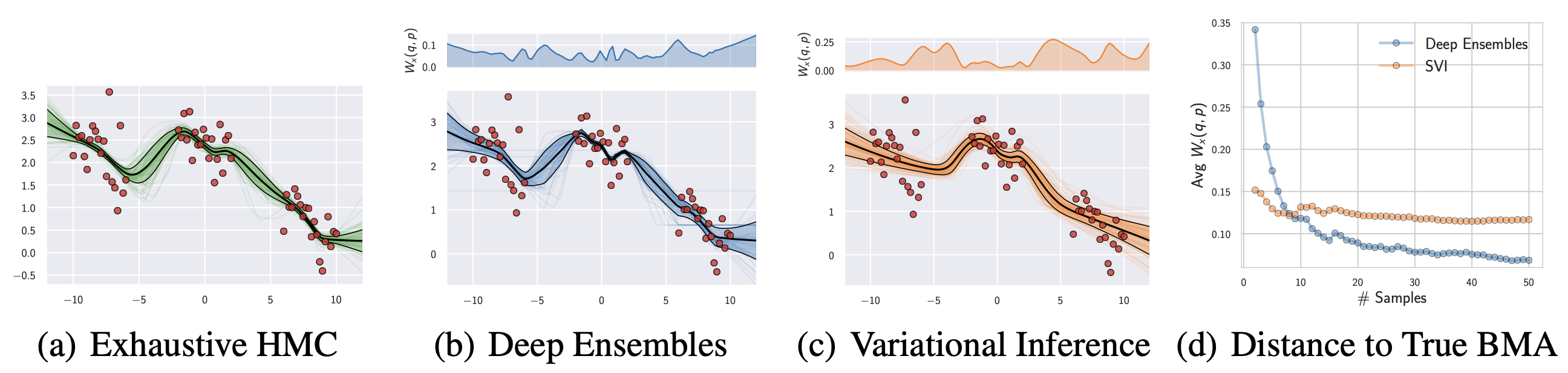
Ground truth로 10 chain의 Hamiltonian Monte Carlo (HMC) 알고리즘을 사용하였으며, 이와 deep ensemble 모델과 variational inference 모델을 비교하였다. Deep ensemble로부터 예측된 분포가 GT와 더 비슷함을 확인할 수 있었으며, 특히 데이터들의 클러스터의 사이 구간에서 deep ensemble은 epistemic uncertainty를 잘 나타냈지만 variational inference의 경우 over-confident한 경향을 나타내었다. 또한, deep ensemble과 GT의 Predictive distribution 간의 Wasserstein distance가 샘플의 수가 늚에 따라 빠르게 감소함을 확인할 수 있었다. 따라서, 이를 통해 deep ensemble이 variational inference에 비해 BMA에 더 가까운 모습을 보여줌을 알 수 있었다.

다음으로, CIFAR-10의 분포 변화에 따른 MultiSWAG (20-samples) 모델의 성능을 평가하였다. 아래 그림에서 왼쪽에서 오른쪽으로 갈 수록 gaussian blur 처리되어 더 corrupt된 이미지이다. 가장 corrupt된 맨 오른쪽 경우에 대해서도 MultiSWAG는 다른 모델들에 비해 낮은 NLL을 보여주었다.

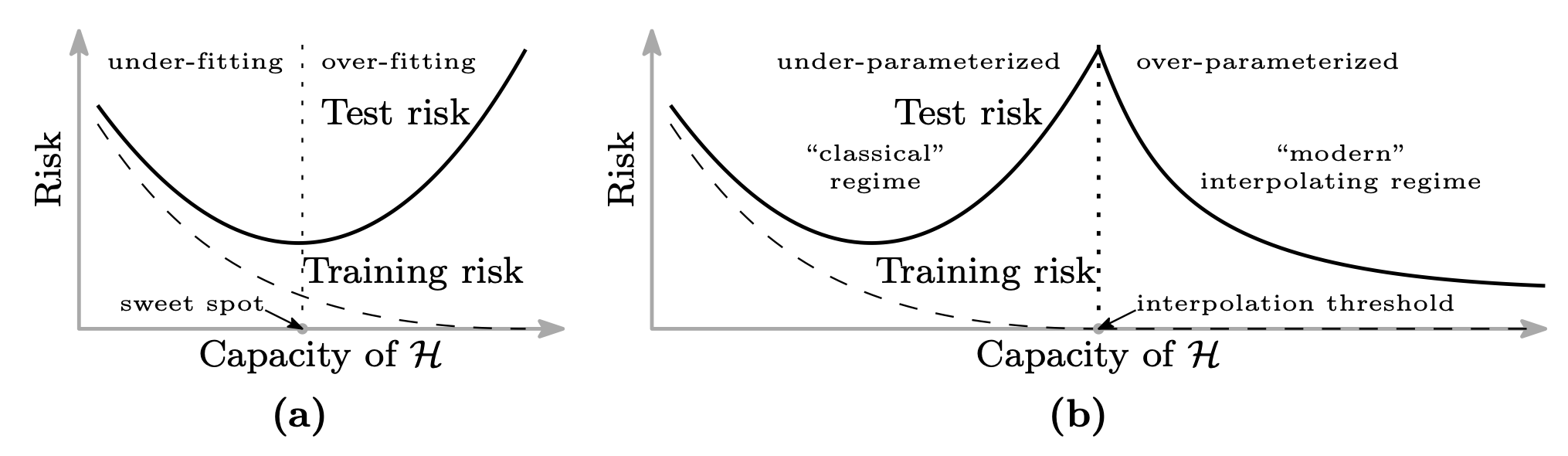
기존의 상식으로는, function class의 capacity가 커져감에 따라 처음에는 under-fitting이 해소되면서 test loss가 감소하다 어느 순간부터는 over-fitting으로 인해 다시 test loss가 증가하는, 아래 그림의 (a) 같은 상황을 생각한다. 하지만 modern regime은 double decent curve를 주장하는데, 이는 capacity의 특정 interpolation threshold를 넘어서면 다시 test risk가 감소한다는 것이다. 이는 기존 심층학습에서 이해할 수 없던 generalization 형태였는데, 본 논문에서의 support, inductive bias의 이차원적인 관점으로는 이를 설명할 수 있다고 주장한다.

아래 그림의 SGD 모델 또한 double decent curve를 보여주고 있다. SWAG 모델은 중간의 test error (또는 NLL) 상승을 완화시켜주며, MultiSWAG 모델에서는 완전히 완화된 모습을 확인할 수 있었다. 또한, 아래 그림 (e)에서 SWAG 모델의 앙상블 개수가 증가함에 따라 점차 중간 피크가 사라지는 것을 확인할 수 있었다. 따라서, 여러 posterior를 marginalize 하는 것이 generalization에 중요함을 시사한다.

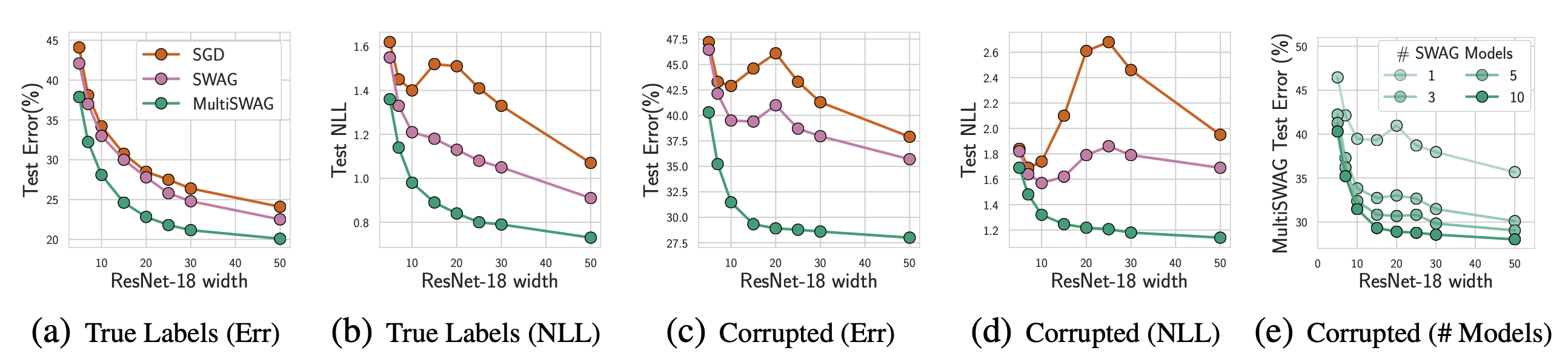
3. Opinion

Deep learning 모델의 generalization이라 하면 over-fitting을 피하는 것이라고만 생각했었는데, 그래서 항상 train loss에 비해 test loss가 잘 줄지 않으면 model의 사이즈를 줄이곤 했다. 하지만, 이 논문은 generalization에서 모델 자체의 성능인 inductive bias 뿐 아니라 basin의 크기인 support 또한 중요하며, 이를 위해 많은 파라미터를 사용할 수 있음을 이야기한다. 특히, 단순히 multi-basin으로 모델을 앙상블해주는 것만으로도 over-fitting으로 인한 double decent를 피할 수 있다는 것이 상당히 인상적이었다.

$$***$$